ちきゅうは1つ? ー地球の「形」について学ぼう

地球の「形」の基本

地球の「形」が球体であることは、みなさんもよくご存じでしょう。そして簡単に「球」と呼んではいるけれども、実際には自転の影響で赤道方向のほうが膨らんでいる「球が少し潰れた形」であることを知っている人も多いと思います。この「少し潰れた球」は平面に描いた楕円をその軸の周りに回転させてできた立体として表され、「回転楕円体」と呼ばれます。

地球の半径はおよそ6,400km、極半径が赤道半径よりも約298分の1だけ短い回転楕円体です。

「ちきゅうは1つ」ではない

人類は自分たちの住む大地がどのような形をしているのかを常に知りたがってきました。地球が平面ではなく球体であることが分かってからも、その大きさを知るためにたくさんの工夫と努力をしてきました。時代により、地域によりそれらの値は変化します。日本国内では、実測による日本地図「大日本沿海輿地全図」を製作した伊能忠敬が有名です。

忠敬は全国地図を作成したことで知られていますが、元々は地球の大きさを知るために「緯度1度」の長さを測りたかったことから北方への測量を願い出たと言われています。元々は勤めていた東京の小石川付近で測っていたのですが、距離が短いと誤差が大きくなるため、より長距離を測ることで誤差を小さくして「真の地球の大きさ」に近づこうとしたのです。

ちなみに、このとき忠敬が求めた緯度1度の長さをキロメートルに直すと、約110.75km。360度を掛けて1周39,870kmでした。現在知られている 約39,940.5kmと比べても遜色ない精度であり、このことからも忠敬らの測量技術の高さが伺い知れますね。

伊能忠敬像(千葉県香取市・伊能忠敬記念館)

ちきゅうを表すモデル

地球をどのような形として見做すことにするかを「モデル」と言います。モデルとは、実際の形と完全に一致するわけではないけれども、こういう形ということにして様々な表現や計算をしましょう、という決めごとです。物理的な地球は1つしかないので、モデルも世界中で統一したただ1つが定められれば十分なように思いますが、各国で様々なモデルが現在も使用されているというのが現状です。長さや重さ、温度などの単位が統一しきれていないのと似ていますね。

日本では、以前は「日本測地系(別名Tokyo測地系)」が使用されていましたが、2002年に「世界測地系(別名JGD: Japanese Geodetic Datum)」へと移行しました。これ以外に、GPSなどで使用されることから米国の「WGS84」もよく使われます。

地球の本当の形はきれいな回転楕円体ではないので(山脈や海溝があるからデコボコであるという話ではありません。地球自体が滑らかではないのです。この話は今後の連載で改めてすることにしましょう)、回転楕円体の曲面をどこに一致させて描くか、というのは様々な方法があります。

日本測地系は日本付近に楕円体の曲面が一致するように調整され、明治時代より採用されてきました。その分、遠く離れた地域、例えばヨーロッパなどにそのまま適用しようとすると差が大きくなってしまうといった課題がありました。時代が進み、日本周辺だけでなく世界とシームレスに繋がる地図表現の必要性から、2002年に改訂されたという経緯があります。「世界測地系」という名前なので誤解されることも多いのですが、日本で使うために日本が定義したものです。この定義の話も、次回以降で少しずつお伝えしていく予定です。

MySQLが知っているちきゅうのいろいろ

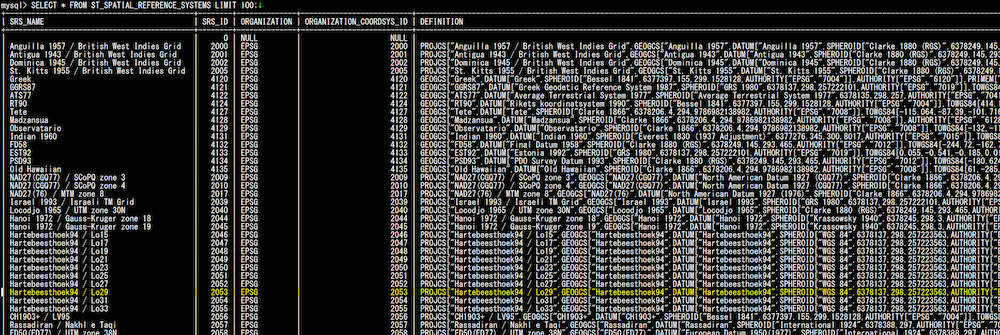
こういった様々な地球の形に関する情報を、MySQLはINFORMATION_SCHEMA内のST_SPATIAL_REFERENCE_SYSTEMSテーブルに持っています。MySQL 9.4.0では、このテーブルに5,238件のデータがあります。

実は、この5,238件の中には「地理座標系」と呼ばれる種類のものと「投影座標系」と呼ばれる種類のものの両方が含まれています。地理座標系とは「丸い地球のモデル」、投影座標系とは「地理座標系を一定の誤差を許容した上で平面に投影した表現法」です。投影座標系については今後の連載で改めて紹介するので、当面は「丸い地球」を表現する地理座標系に焦点を当てていきたいと思います。

地理座標系のデータは、DEFINITION列の値が“GEOGCS”で開始されています(投影座標系は“PROJCS”です)。地理座標系のデータだけをカウントすると545件になります。圧倒的に投影座標系のほうが多い理由も、測地系についての学びを進めていくうちに自然に分かることでしょう。

mysql> SELECT LEFT(DEFINITION,6) cs, COUNT(*) 
    ->   FROM ST_SPATIAL_REFERENCE_SYSTEMS
    ->  GROUP BY LEFT(DEFINITION,6);
+--------+----------+
| cs     | COUNT(*) |
+--------+----------+
|        |        1 |
| PROJCS |     4692 |
| GEOGCS |      545 |
+--------+----------+
3 rows in set (0.002 sec)

このテーブルで見るべきカラムはSRS_NAME、SRS_ID、DEFINITIONの3つです。SRS_NAMEは測地系の名前で、主に人間が目で見て確認するためのものです。SRS_IDはその定義を特定するためのユニークな番号で、実際に地理情報データを操作する際にコマンドの中でも頻繁に使用します。DEFINITION列がモデルの定義で、地球のサイズやその他の大切な情報が含まれています。

次回は、このST_SPATIAL_REFERENCE_SYSTEMSテーブルにどのようなデータが定義されているのかを、日本に関する定義を例に紹介していきます。