2D〜4Dで向きや大きさを持つ数字の集まり「ベクトル」について学ぼう

三次元ベクトルの特殊な計算

次のベクトルの特殊な計算「ベクトルの長さ」「ベクトルの正規化」「内積」「外積」「ベクトルの増分」については、「class Vector3D { ここ }」の中にコーディングしてください。具体的な実装方法は、次のURLの「DOWNLOAD」からサンプルをダウンロードしてください。

・UltraMotion3DのWebサイト(※必ずパソコンのGoogle Chromeで見てください)
https://webgpu.roxiga.com

ベクトルの長さ

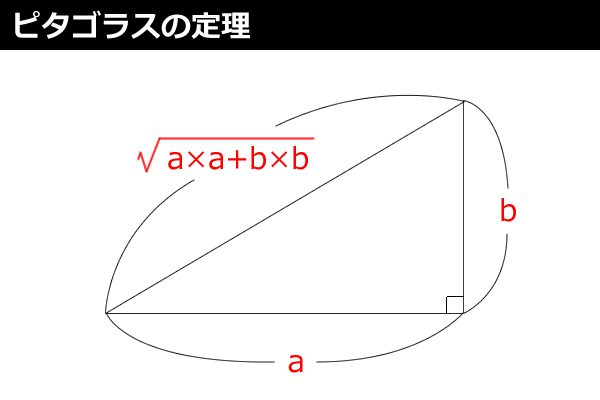
ベクトルの長さ(距離)を計算するには「ピタゴラスの定理」を使います(図2)。ここでは二次元の距離を求めていますが、三次元では(X*X+Y*Y+Z*Z)の平方根を求めます。

・サンプルコード「lib」→「Vector3D.js」

  length() {
    return Math.sqrt(this.x*this.x + this.y*this.y + this.z*this.z);
  }

【サンプルコードの解説】
【サンプルコードの解説】
「length」メソッドでxプロパティの2乗とyプロパティの2乗、zプロパティの2乗を足したルート(sqrt関数)を戻り値にスカラで返します。

ベクトルの正規化

「正規化(ノーマライズ)」とは、ベクトルの長さを1にすることです。ベクトルをベクトルの長さで除算すると、長さ1のベクトルに変換できます。もしベクトルの長さが0の場合は、数学で0の除算(ZeroDivide)はあり得ないため場合分けをします。よく考えると、ここはベクトルの除算をしていました(汗)。

・サンプルコード「lib」→「Vector3D.js」

  normalize() {
    var l = this.length();
    if ( l == 0 ) {
      this.x = 0;
      this.y = 0;
      this.z = 1;
    } else {
      this.x /= l;
      this.y /= l;
      this.z /= l;
    }
  }

【サンプルコードの解説】
「normalize」メソッドでベクトルの長さを取得し、その長さが0の場合は(X,Y,Z)=(0,0,1)にして0以外はベクトルを長さで除算します。

内積

「内積(Dot Product)」は、2つのベクトルの向きの違いなどを調べることができます。AとBの内積を「A・B」のようにDot(ドット)で表記します。例えば、2つのベクトルが垂直より同じ方向に近いか反対向きに近いかをスカラで調べられます。

・サンプルコード「lib」→「Vector3D.js」

  dotProduct(v) {
    return (v.x * this.x + v.y * this.y + v.z * this.z);
  }

【サンプルコードの解説】
「dotProduct」メソッドでX1*X2+Y1*Y2+Z1*Z2を計算して内積を求め、戻り値で返します。

外積

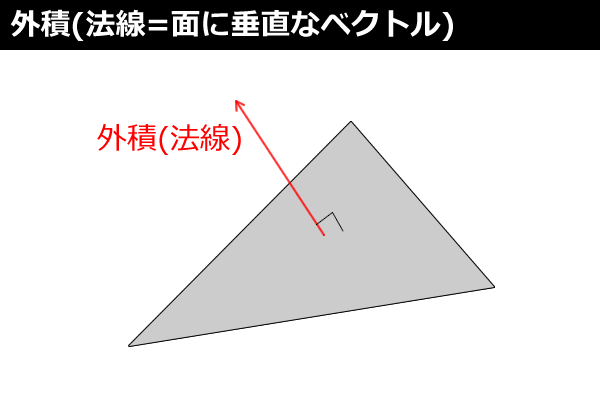
外積(Cross Product)は2つのベクトルで表される平面に垂直なベクトル(法線)を求める計算です(図3)。AとBの外積を「A×B」のようにCross(クロス)で表記します。

・サンプルコード「lib」→「Vector3D.js」

  crossProduct(v) {
    const x = (this.y*v.z) - (this.z*v.y);
    const y = (this.z*v.x) - (this.x*v.z);
    const z = (this.x*v.y) - (this.y*v.x);
    return new Vector3D(x,y,z);
  }

【サンプルコードの解説】
「crossProduct」メソッドで(X,Y,Z)=(Y1*Z2-Z1*Y2,Z1*X2-X1*Z2,X1*Y2-Y1*X2)を計算して外積を求め、戻り値でそのベクトルを返します。

その他のベクトルの増分の計算

このUltraMotion3Dライブラリで使うその他の計算も実装しておきましょう。デルタ(増分)だけXとYとZに加算したとき、0度より小さければ360度加算し、360度以上なら360度減算して必ず0～360度未満にします。

・サンプルコード「lib」→「Vector3D.js」

  addX(delta) {
    this.x += delta;
    if ( this.x < 0 ) this.x += 360;
    if ( this.x >= 360 ) this.x -= 360;
  }
  addY(delta) {
    this.y += delta;
    if ( this.y < 0 ) this.y += 360;
    if ( this.y >= 360 ) this.y -= 360;
  }
  addZ(delta) {
    this.z += delta;
    if ( this.z < 0 ) this.z += 360;
    if ( this.z >= 360 ) this.z -= 360;
  }

【サンプルコードの解説】
「addX」メソッドでxプロパティにdelta引数を加算し、0より小さければ360加算し、360以上なら360減算します。
「addY」メソッドでyプロパティにdelta引数を加算し、0より小さければ360加算し、360以上なら360減算します。
「addZ」メソッドでzプロパティにdelta引数を加算し、0より小さければ360加算し、360以上なら360減算します。

おわりに

今回は二次元(2D)ベクトルの(X,Y)と三次元(3D)ベクトルの(X,Y,Z)、四次元(4D)ベクトルの(X,Y,Z,W)について、基礎知識とその計算方法について解説しました。

次回は「行列」を取り上げます。具体的には「三角関数」と「行列の計算の実装」について解説します。