2D〜4Dで向きや大きさを持つ数字の集まり「ベクトル」について学ぼう

はじめに

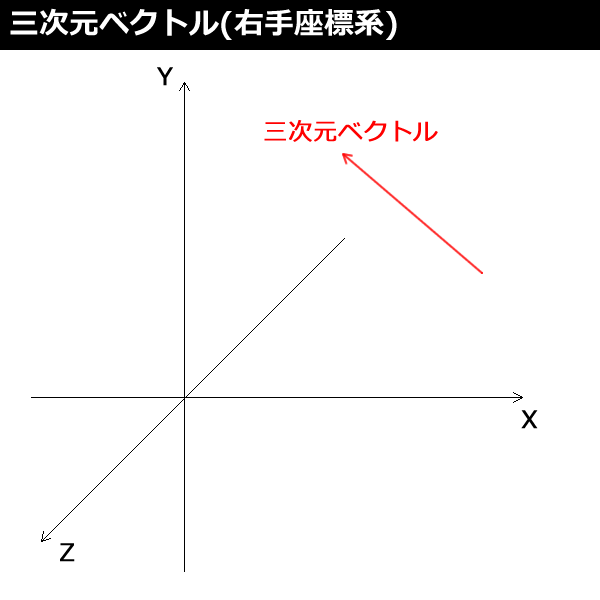
今回は「ベクトル」と、ベクトルの最低限必要な実装について解説します。普通の数字のことを「スカラ」と呼びますが、図1のようにベクトルは向きや大きさを持つ数字の集まりで、一般に「二次元」「三次元」「四次元」のベクトルがあります。作ろうと思えば何次元でもベクトルにできると思いますが、基本的に3DCGではこの3つだけです。

図1：三次元ベクトルの概要

ベクトルとは

二次元(2D)ベクトルは(X,Y)、三次元(3D)ベクトルは(X,Y,Z)、四次元(4D)ベクトルは(X,Y,Z,W)で表されます。高校の数学で習うので皆さんもご存知でしょう。四次元ベクトルは高校数学では習いませんが、三次元ベクトルと同じように使います。四次元ベクトルは三次元ベクトルに1つ「W」座標のオマケが付いています(後述)。

それでは、これらのベクトルをプログラミングして、使えるようになりましょう。

二次元ベクトル

横のX座標と縦のY座標がある二次元で向きや大きさを持つのが二次元ベクトルです。「横にいくら進んだか」「縦にいくら進んだか」「どれだけの距離進んだか」を表します。また原点0からどの方向にどれだけ進んだかで頂点の座標を表すこともできます。モニターの画面はまさに横と縦しかない二次元です。

class Vector2D {
  constructor(x,y) {
    this.x = x;
    this.y = y;
  }
}

let v = new Vector2D(0,0);

三次元ベクトル

横のX座標と縦のY座標、奥行きのZ座標がある三次元で向きや大きさを持つのが三次元ベクトルです。「横にいくら進んだか」「縦にいくら進んだか」「手前奥にいくら進んだか」「どれだけの距離進んだか」を表します。また原点0からどの方向にどれだけ進んだかで頂点の座標を表すこともできます。ちょっと話は逸れますが、よく耳にする「3DCG」は表示するモニター画面は横と縦しかない二次元なので、結局2DCGの一種と言えます。

class Vector3D {
  constructor(x,y,z) {
    this.x = x;
    this.y = y;
    this.z = z;
  }
}

let v = new Vector3D(0,0,0);

四次元ベクトル

横のX座標と縦のY座標、奥行きのZ座標と、さらにもう1つW座標がある四次元で向きや大きさを持つのが四次元ベクトルです。XYZについては三次元ベクトルと同じく、「横にいくら進んだか」「縦にいくら進んだか」「手前奥にいくら進んだか」「どれだけの距離進んだか」を表します。また原点0からどの方向にどれだけ進んだかで頂点の座標を表すこともできます。

厳密には違うと思いますが、次回で解説する「行列」は4行×4列で、ベクトルを行列に乗算するには4列のベクトルがなくては計算できません。そのため四次元ベクトルが必要になります。Wの値が1のとき(X,Y,Z)は平行移動を表し、それ以外のときは回転を表します。

class Vector4D {
  constructor(x,y,z,w) {
    this.x = x;
    this.y = y;
    this.z = z;
    this.w = w;
  }
}

let v = new Vector4D(0,0,0,1);

三次元ベクトルの四則演算

ベクトルの加算には「add」関数を、減算には「subtract」関数を、乗算には「mul」関数を実装します(UltraMotion3Dではベクトルの除算を使用しないため省略)。

なお、次のサンプルコードでベクトルの加減乗除を計算する際は「class Vector3D { ここ }」の中にコーディングしてください。

  add(v) {
    const x = this.x + v.x;
    const y = this.y + v.y;
    const z = this.z + v.z;
    return new Vector3D(x,y,z);
  }
  subtract(v) {
    const x = this.x - v.x;
    const y = this.y - v.y;
    const z = this.z - v.z;
    return new Vector3D(x,y,z);
  }
  mul(v) {
    const x = this.x * v;
    const y = this.y * v;
    const z = this.z * v;
    return new Vector3D(x,y,z);
  }

【サンプルコードの解説】
add関数はベクトル同士の加算で(X,Y,Z)=(X1+X2,Y1+Y2,Z1+Z2)です。
subtract関数はベクトル同士の減算で(X,Y,Z)=(X1-X2,Y1-Y2,Z1-Z2)です。
mul関数はベクトルにスカラを乗算する計算で(X,Y,Z)=(X1*値1,Y1*値1,Z1*値1)です。