3Dの移動や回転、拡大・縮小する「行列」について学ぼう

移動行列

「移動」と言うと平行移動だけを想像しがちですが、回転移動やスケーリング移動も入ります。平行移動と回転、スケーリング行列を計算して1つにまとめた行列のことを「アフィン変換行列」と言います。

回転にはX軸を中心に回転する計算、Y軸を中心に回転する計算、Z軸を中心に回転する計算の3つがあります。スカラの乗算は順番が違っても変化ありませんが、平行移動、XYZ軸回転、スケーリングの行列を乗算する順番により結果が異なることに注意してください。回転の順番によっても結果が変わります。

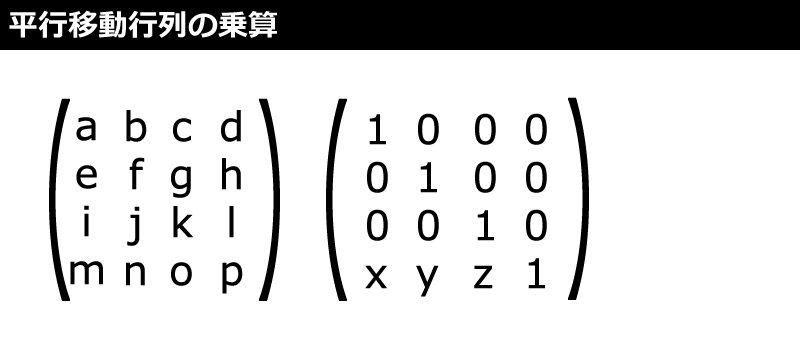
平行移動行列

平行移動とは、回転もスケーリングもせず真っすぐ頂点の位置が移動することです。計算方法は、図4のように次のサンプルコードの「translate」メソッドの通りです。translateとは「移す」という意味です。これも行列同士を乗算して計算します。

・サンプルコード「lib」→「Matrix3D.js」

  translate(v) {
    var a00,a01,a02,a03,a10,a11,a12,a13,a20,a21,a22,a23;
    a00 = this.e[0]; a01 = this.e[1]; a02 = this.e[ 2]; a03 = this.e[ 3];
    a10 = this.e[4]; a11 = this.e[5]; a12 = this.e[ 6]; a13 = this.e[ 7];
    a20 = this.e[8]; a21 = this.e[9]; a22 = this.e[10]; a23 = this.e[11];
    this.e[0] = a00; this.e[1] = a01; this.e[ 2] = a02; this.e[ 3] = a03;
    this.e[4] = a10; this.e[5] = a11; this.e[ 6] = a12; this.e[ 7] = a13;
    this.e[8] = a20; this.e[9] = a21; this.e[10] = a22; this.e[11] = a23;
    this.e[12] = a00 * v.x + a10 * v.y + a20 * v.z + this.e[12];
    this.e[13] = a01 * v.x + a11 * v.y + a21 * v.z + this.e[13];
    this.e[14] = a02 * v.x + a12 * v.y + a22 * v.z + this.e[14];
    this.e[15] = a03 * v.x + a13 * v.y + a23 * v.z + this.e[15];
  }

【サンプルコードの解説】
単位行列に似ており、他に変化があるのは4行目だけです。
戻り値でMatrix3Dのインスタンスを返すのではなく、自分自身の4×4行列のプロパティ数値を計算しています。

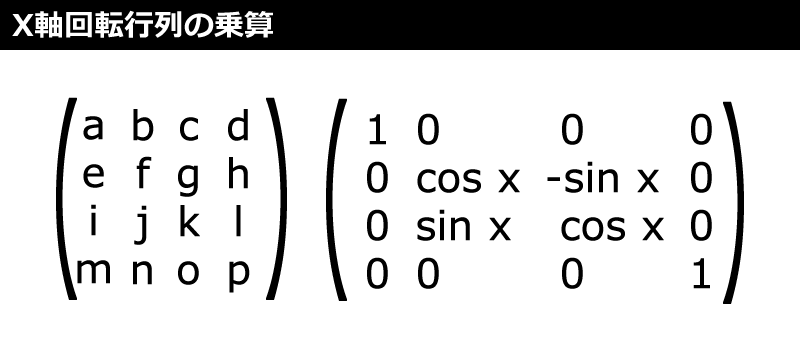
X軸回転行列

X軸を中心に回転する行列の計算方法は、図5のように次のサンプルコードの「rotateX」メソッドの通りです。頂点のポイント自体が回転するわけではなく、X軸を中心に頂点の位置が回転するわけです。これも行列同士を乗算して計算します。

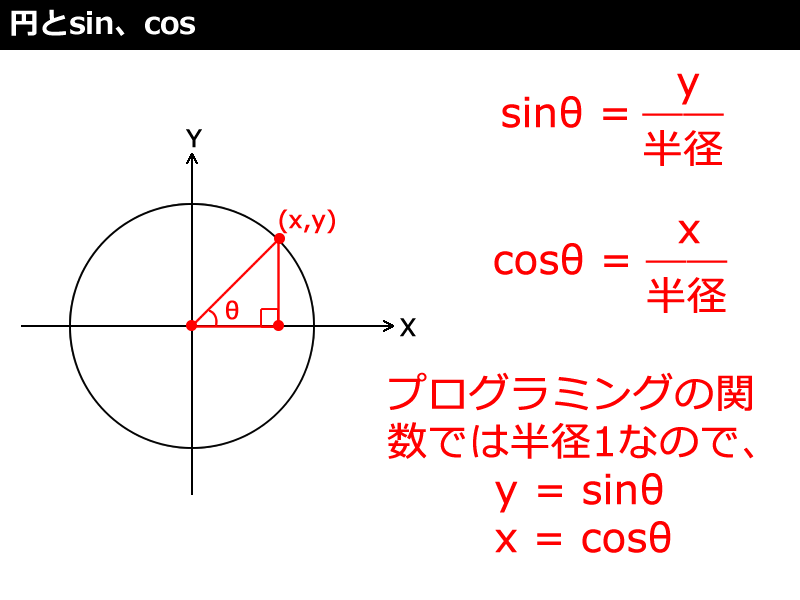
言うまでもなく図6のようにMath.sin(ラジアン)で「サイン」の数値を取得でき、Math.cos(ラジアン)で「コサイン」の数値を取得できます。ただ、大抵のプログラミング言語では「半径=1」としてsin、cosの値が取得できます。

・サンプルコード「lib」→「Matrix3D.js」

  rotateX(angle) {
    var s = Math.sin(angle);
    var c = Math.cos(angle);
    var a10 = this.e[4];
    var a11 = this.e[5];
    var a12 = this.e[6];
    var a13 = this.e[7];
    var a20 = this.e[8];
    var a21 = this.e[9];
    var a22 = this.e[10];
    var a23 = this.e[11];
    this.e[4] = a10 * c + a20 * s;
    this.e[5] = a11 * c + a21 * s;
    this.e[6] = a12 * c + a22 * s;
    this.e[7] = a13 * c + a23 * s;
    this.e[8] = a10 * -s + a20 * c;
    this.e[9] = a11 * -s + a21 * c;
    this.e[10] = a12 * -s + a22 * c;
    this.e[11] = a13 * -s + a23 * c;
  }

【サンプルコードの解説】
「angle」引数は「ディグリー」角度ではなく「ラジアン」角度です。
戻り値でMatrix3Dのインスタンスを返すのではなく、自分自身の4×4行列のプロパティ数値を計算しています。

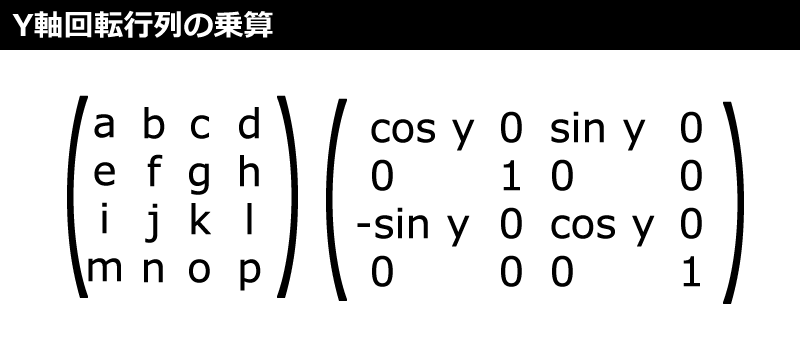
Y軸回転行列

Y軸を中心に回転する行列の計算方法は、図7のように次のサンプルコードの「rotateY」メソッドの通りです。頂点のポイント自体が回転するわけではなく、Y軸を中心に頂点の位置が回転するわけです。これも行列同士を乗算して計算します。

・サンプルコード「lib」→「Matrix3D.js」

  rotateY(angle) {
    var s = Math.sin(angle);
    var c = Math.cos(angle);
    var a00 = this.e[0];
    var a01 = this.e[1];
    var a02 = this.e[2];
    var a03 = this.e[3];
    var a20 = this.e[8];
    var a21 = this.e[9];
    var a22 = this.e[10];
    var a23 = this.e[11];
    this.e[0] = a00 * c + a20 * -s;
    this.e[1] = a01 * c + a21 * -s;
    this.e[2] = a02 * c + a22 * -s;
    this.e[3] = a03 * c + a23 * -s;
    this.e[8] = a00 * s + a20 * c;
    this.e[9] = a01 * s + a21 * c;
    this.e[10] = a02 * s + a22 * c;
    this.e[11] = a03 * s + a23 * c;
  }

【サンプルコードの解説】
angle引数はディグリー角度ではなくラジアン角度です。
戻り値でMatrix3Dのインスタンスを返すのではなく、自分自身の4×4行列のプロパティ数値を計算しています。

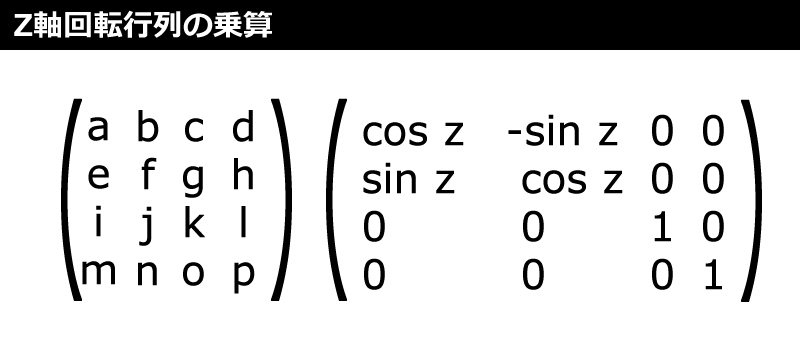
Z軸回転行列

Z軸を中心に回転する行列の計算方法は、図8のように次のサンプルコードの「rotateZ」メソッドの通りです。頂点のポイント自体が回転するわけではなく、Z軸を中心に頂点の位置が回転するわけです。これも行列同士を乗算して計算します。

・サンプルコード「lib」→「Matrix3D.js」

  rotateZ(angle) {
    var s = Math.sin(angle);
    var c = Math.cos(angle);
    var a00 = this.e[0];
    var a01 = this.e[1];
    var a02 = this.e[2];
    var a03 = this.e[3];
    var a10 = this.e[4];
    var a11 = this.e[5];
    var a12 = this.e[6];
    var a13 = this.e[7];
    this.e[0] = a00 * c + a10 * s;
    this.e[1] = a01 * c + a11 * s;
    this.e[2] = a02 * c + a12 * s;
    this.e[3] = a03 * c + a13 * s;
    this.e[4] = a00 * -s + a10 * c;
    this.e[5] = a01 * -s + a11 * c;
    this.e[6] = a02 * -s + a12 * c;
    this.e[7] = a03 * -s + a13 * c;
  }

【サンプルコードの解説】
angle引数はディグリー角度ではなくラジアン角度です。
戻り値でMatrix3Dのインスタンスを返すのではなく、自分自身の4×4行列のプロパティ数値を計算しています。

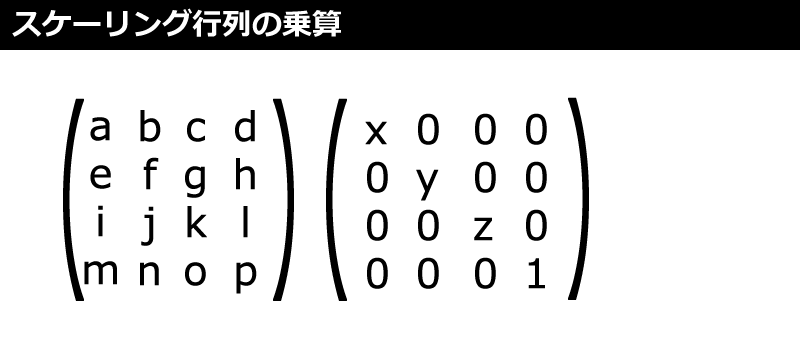
スケーリング行列

拡大縮小するスケーリング行列の計算方法は、図9のように次のサンプルコード「scale」メソッドの通りです。頂点のポイント自体が大きくなるわけではなく、中心から見て頂点の位置が拡大縮小するわけです。これも行列同士を乗算して計算します。

・サンプルコード「lib」→「Matrix3D.js」

  scale(v) {
    this.e[ 0] *= v.x;
    this.e[ 1] *= v.x;
    this.e[ 2] *= v.x;
    this.e[ 3] *= v.x;
    this.e[ 4] *= v.y;
    this.e[ 5] *= v.y;
    this.e[ 6] *= v.y;
    this.e[ 7] *= v.y;
    this.e[ 8] *= v.z;
    this.e[ 9] *= v.z;
    this.e[10] *= v.z;
    this.e[11] *= v.z;
  }

【サンプルコードの解説】
戻り値でMatrix3Dのインスタンスを返すのではなく、自分自身の4×4行列のプロパティ数値を計算しています。