3Dの移動や回転、拡大・縮小する「行列」について学ぼう

ビューとパースペクティブ

「ビュー」はカメラの「視点」と「注視点」と「上向きベクトル」を元に、カメラを3Dモデルなどに向ける行列です。カメラ視点はカメラの目の位置、カメラ注視点はカメラがどの座標に向いているか、上向きベクトルはカメラ自体の傾きです。

「パースペクティブ」は遠近法をかける行列です。これで3Dモデルがより立体的によりリアルな大きさで表示できます。一般的に3Dプログラミングでは、まず頂点に移動行列(平行移動、回転、スケーリング)、次にビュー行列、最後にプロジェクション行列(ここではパースペクティブ行列)を乗算します(図10)。

カメラビュー行列

カメラの視点から注視点の方を向けるには、図11のようにビュー行列を乗算します。一見カメラが向いているように思われますが、モデル全てを移動させてカメラが向いているように見せています。これも行列同士を乗算して計算します。

・サンプルコード「lib」→「Matrix3D.js」

  lookAt(eye, at, up) {
    var z2 = eye.subtract(at);
    z2.normalize();
    var x2 = up.crossProduct(z2);
    x2.normalize();
    var y2 = z2.crossProduct(x2);
    this.e[ 0] = x2.x;
    this.e[ 1] = y2.x;
    this.e[ 2] = z2.x;
    this.e[ 3] = 0;
    this.e[ 4] = x2.y;
    this.e[ 5] = y2.y;
    this.e[ 6] = z2.y;
    this.e[ 7] = 0;
    this.e[ 8] = x2.z;
    this.e[ 9] = y2.z;
    this.e[10] = z2.z;
    this.e[11] = 0;
    this.e[12] = -x2.dotProduct(eye);
    this.e[13] = -y2.dotProduct(eye);
    this.e[14] = -z2.dotProduct(eye);
    this.e[15] = 1;
  }

透視投影変換行列

「透視投影」とは、近くのものは大きく、遠くのものは小さく見せる遠近法をかける計算です。よく「パースをかける」と言いますが、これは「Perspective(パースペクティブ、遠近法)」から来ています。図12のように透視投影変換行列を乗算します。これも行列同士を乗算して計算します。

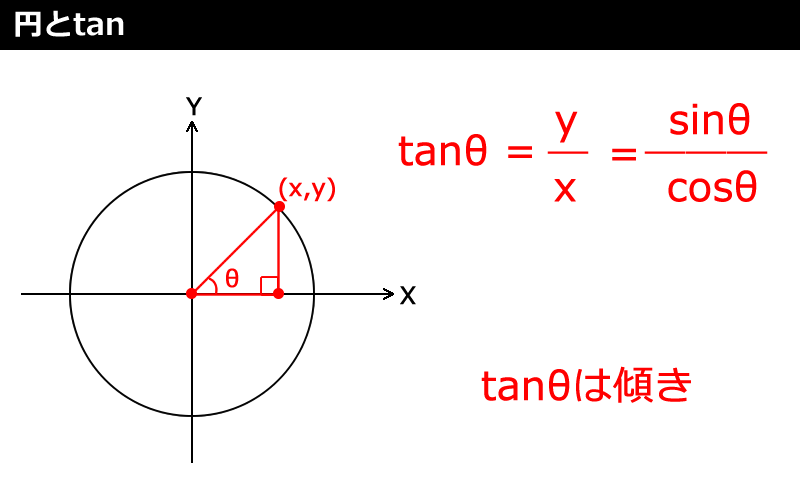
図12の「top」「bottom」「right」「left」は、次のサンプルコードのように計算します。「fov」引数は「視野角」、「aspect」引数は「アスペクト比(縦横比)」を「near(近く)」～「far(遠く)」の間まで3D描画します。基本的なことですが、図13のように「Math.tan(ラジアン)」の「タンジェント」についても解説します。

・サンプルコード「lib」→「Matrix3D.js」

  perspective(fov, aspect, near, far) {
    let top = near * Math.tan(fov * Math.PI / 360.0);
    let bottom = -top;
    let right = top * aspect;
    let left = -right;
    let rl = (right - left);
    let tb = (top - bottom);
    let fn = (far - near);
    this.e[ 0] = (near * 2) / rl;
    this.e[ 1] = 0;
    this.e[ 2] = 0;
    this.e[ 3] = 0;
    this.e[ 4] = 0;
    this.e[ 5] = (near * 2) / tb;
    this.e[ 6] = 0;
    this.e[ 7] = 0;
    this.e[ 8] = (right + left) / rl;
    this.e[ 9] = (top + bottom) / tb;
    this.e[10] = -(far + near) / fn;
    this.e[11] = -1;
    this.e[12] = 0;
    this.e[13] = 0;
    this.e[14] = -(far * near * 2) / fn;
    this.e[15] = 0;
  }

【サンプルコードの解説】
top変数は「near * Math.tan(fov * Math.PI / 360.0)」と計算します。
bottom変数はtop変数のマイナスです。
right変数はtop変数をアスペクト比から求められます。
left変数はright変数のマイナスです。

その他の行列計算

その他にも最低限知っておくべき行列計算として「逆行列(インバース)」と「転置(トランスポーズ)」があります。

逆行列

「逆行列」は図14のような行列式が成り立つ行列のことです。ある行列に逆行列を乗算すると単位行列になります。「inverse」は「逆数」「逆の」を意味する英語です。計算方法は次のサンプルコードの通りです。

ここで、inverseメソッドに「static」が付いていますが、スタティックメソッドはインスタンスを生成しなくても、ここでは「Matrix3D.inverse(引数)」のように「クラス名.メソッド名()」で呼び出せるメソッドのことです。

・サンプルコード「lib」→「Matrix3D.js」

  static inverse(mat) {
    var matrix = new Matrix3D();
    var a = mat.e[0],  b = mat.e[1],  c = mat.e[2],  d = mat.e[3],
      e = mat.e[4],  f = mat.e[5],  g = mat.e[6],  h = mat.e[7],
      i = mat.e[8],  j = mat.e[9],  k = mat.e[10], l = mat.e[11],
      m = mat.e[12], n = mat.e[13], o = mat.e[14], p = mat.e[15],
      q = a * f - b * e, r = a * g - c * e,
      s = a * h - d * e, t = b * g - c * f,
      u = b * h - d * f, v = c * h - d * g,
      w = i * n - j * m, x = i * o - k * m,
      y = i * p - l * m, z = j * o - k * n,
      A = j * p - l * n, B = k * p - l * o,
      ivd = 1 / (q * B - r * A + s * z + t * y - u * x + v * w);
    matrix.e[ 0] = ( f * B - g * A + h * z) * ivd;
    matrix.e[ 1] = (-b * B + c * A - d * z) * ivd;
    matrix.e[ 2] = ( n * v - o * u + p * t) * ivd;
    matrix.e[ 3] = (-j * v + k * u - l * t) * ivd;
    matrix.e[ 4] = (-e * B + g * y - h * x) * ivd;
    matrix.e[ 5] = ( a * B - c * y + d * x) * ivd;
    matrix.e[ 6] = (-m * v + o * s - p * r) * ivd;
    matrix.e[ 7] = ( i * v - k * s + l * r) * ivd;
    matrix.e[ 8] = ( e * A - f * y + h * w) * ivd;
    matrix.e[ 9] = (-a * A + b * y - d * w) * ivd;
    matrix.e[10] = ( m * u - n * s + p * q) * ivd;
    matrix.e[11] = (-i * u + j * s - l * q) * ivd;
    matrix.e[12] = (-e * z + f * x - g * w) * ivd;
    matrix.e[13] = ( a * z - b * x + c * w) * ivd;
    matrix.e[14] = (-m * t + n * r - o * q) * ivd;
    matrix.e[15] = ( i * t - j * r + k * q) * ivd;
    return matrix;
  }

転置

「transpose」は「転置(行と列の成分を入れ替えること)」を意味する英語です。よくExcelで使われるので、ご存知の方も多いでしょう。1行2列の成分と2行1列の成分を入れ替え、1行3列の成分と3行1列の成分を入れ替え…、というように4×4成分全て転置します。

・サンプルコード「lib」→「Matrix3D.js」

  transpose() {
    var mat = new Matrix3D();
    mat.e[ 0] = this.e[ 0];
    mat.e[ 1] = this.e[ 4];
    mat.e[ 2] = this.e[ 8];
    mat.e[ 3] = this.e[12];
    mat.e[ 4] = this.e[ 1];
    mat.e[ 5] = this.e[ 5];
    mat.e[ 6] = this.e[ 9];
    mat.e[ 7] = this.e[13];
    mat.e[ 8] = this.e[ 2];
    mat.e[ 9] = this.e[ 6];
    mat.e[10] = this.e[10];
    mat.e[11] = this.e[14];
    mat.e[12] = this.e[ 3];
    mat.e[13] = this.e[ 7];
    mat.e[14] = this.e[11];
    mat.e[15] = this.e[15];
    return mat;
  }

おわりに

今回は「行列」について解説しました。また、実際に行列を使って平行移動や回転や拡大縮小したり、カメラ視点を変換したり、遠近法で変換したりしてみました。

次回は「シェーダー」の文法について解説します。