3Dの移動や回転、拡大・縮小する「行列」について学ぼう

はじめに

今回は頂点のベクトル座標を移動(平行移動行列・XYZ軸回転行列・スケーリング行列)したり、カメラの視線に合わせて変形(ビュー行列)したり、遠近法で変形(パースペクティブ行列)したりする「行列」の計算を実装します。次回のテーマである「シェーダー」では行列計算の中身までは出てこないので、ここで行列の計算について見ていきましょう。

行列

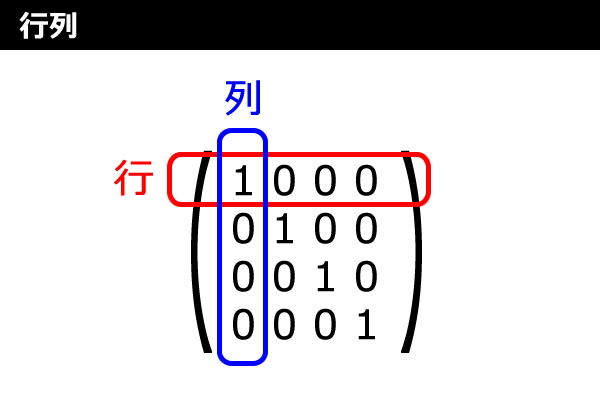
行列とは、図1のように「行」と「列」で表されたベクトルのようなものです。3DCGでは大抵4×4行列(4行4列)です。後ほどコラムにも書きますが、実は筆者も計算方法を知ってるだけで、それほど深くそれぞれの行列計算の意味を知っているわけではありません。それでも、本連載のように「UltraMotion3D」ライブラリだって作れてしまいます。メソッドさえ使いこなせるなら、中身まで詳しく知らなくても何とかなるものです。

行列の初期化

行列は全くの0だけで初期化するわけではありません。先の図1のように、コンストラクタで「単位行列」というスカラでいう「1」に似た数値で初期化します。前回に引き続きもう一度説明しますが、スカラとはベクトルなどの数値の集まりに対し、単なる数字のことを言います。

・サンプルコード「lib」→「Matrix3D.js」

class Matrix3D {
  constructor(e) {
    this.e = new Float32Array([
      1,0,0,0,
      0,1,0,0,
      0,0,1,0,
      0,0,0,1]);
  }
}

【サンプルコードの解説】
「Float32Array」は「型付き配列(TypedArray)」の一種で、32ビットの浮動小数点数の配列を扱います。高速な数値計算の操作に使われ、一般のJavaScriptの配列とは異なります。

単位行列

今回の以降のメソッドは「class Matrix3D { ここ }」に追記します。コンストラクタと全く同じですが、一応単位行列の「identity」メソッドも用意しておきます。単位行列にどんな行列を乗算しても元の行列と同じ行列になるのが単位行列です。

・サンプルコード「lib」→「Matrix3D.js」

  identity() {
    this.e = new Float32Array([
      1,0,0,0,
      0,1,0,0,
      0,0,1,0,
      0,0,0,1]);
  }

ベクトルのトランスフォーム

3DCGにおいて、行列は大抵ベクトルと行列は乗算します(図2)。ベクトルと行列はあまり加算したり減算したり除算したりしません。後述する「アフィン変換行列」「ビュー行列」「パースペクティブ行列」を乗算した行列で、3D頂点のベクトル座標をトランスフォームして変換します。

・サンプルコード「lib」→「Matrix3D.js」

  transform(v) {
    var x = v.x * this.e[0] + v.y * this.e[4] + v.z * this.e[8]  + v.w * this.e[12];
    var y = v.x * this.e[1] + v.y * this.e[5] + v.z * this.e[9]  + v.w * this.e[13];
    var z = v.x * this.e[2] + v.y * this.e[6] + v.z * this.e[10] + v.w * this.e[14];
    var w = v.x * this.e[3] + v.y * this.e[7] + v.z * this.e[11] + v.w * this.e[15];
    return new Vector4D(x,y,z,w);
  }

【サンプルコードの解説】
「transform(トランスフォーム)」というメソッド名は、ベクトルに行列を乗算することでベクトルを「変形」するからです。
「v」引数は「Vector4D」クラスのインスタンスでなくてはならず、ベクトルに行列を乗算したVector4Dクラスのインスタンスを戻り値で返します。

行列同士の乗算

3DCGにおいて、行列は大抵行列同士を乗算します(図3)。行列同士はあまり加算したり減算したり除算したりしません。今回のサンプルコードのようにたくさん計算量があるので、次回で説明するシェーダーでは行列計算をハードウェア(グラフィックボード、ビデオカード)で計算して処理を高速化するわけです。

・サンプルコード「lib」→「Matrix3D.js」

  static multiply(a,b) {
    const matrix = new Matrix3D();
    matrix.e[ 0] = a.e[ 0]*b.e[0] + a.e[ 1]*b.e[4] + a.e[ 2]*b.e[ 8] + a.e[ 3]*b.e[12];
    matrix.e[ 1] = a.e[ 0]*b.e[1] + a.e[ 1]*b.e[5] + a.e[ 2]*b.e[ 9] + a.e[ 3]*b.e[13];
    matrix.e[ 2] = a.e[ 0]*b.e[2] + a.e[ 1]*b.e[6] + a.e[ 2]*b.e[10] + a.e[ 3]*b.e[14];
    matrix.e[ 3] = a.e[ 0]*b.e[3] + a.e[ 1]*b.e[7] + a.e[ 2]*b.e[11] + a.e[ 3]*b.e[15];
    matrix.e[ 4] = a.e[ 4]*b.e[0] + a.e[ 5]*b.e[4] + a.e[ 6]*b.e[ 8] + a.e[ 7]*b.e[12];
    matrix.e[ 5] = a.e[ 4]*b.e[1] + a.e[ 5]*b.e[5] + a.e[ 6]*b.e[ 9] + a.e[ 7]*b.e[13];
    matrix.e[ 6] = a.e[ 4]*b.e[2] + a.e[ 5]*b.e[6] + a.e[ 6]*b.e[10] + a.e[ 7]*b.e[14];
    matrix.e[ 7] = a.e[ 4]*b.e[3] + a.e[ 5]*b.e[7] + a.e[ 6]*b.e[11] + a.e[ 7]*b.e[15];
    matrix.e[ 8] = a.e[ 8]*b.e[0] + a.e[ 9]*b.e[4] + a.e[10]*b.e[ 8] + a.e[11]*b.e[12];
    matrix.e[ 9] = a.e[ 8]*b.e[1] + a.e[ 9]*b.e[5] + a.e[10]*b.e[ 9] + a.e[11]*b.e[13];
    matrix.e[10] = a.e[ 8]*b.e[2] + a.e[ 9]*b.e[6] + a.e[10]*b.e[10] + a.e[11]*b.e[14];
    matrix.e[11] = a.e[ 8]*b.e[3] + a.e[ 9]*b.e[7] + a.e[10]*b.e[11] + a.e[11]*b.e[15];
    matrix.e[12] = a.e[12]*b.e[0] + a.e[13]*b.e[4] + a.e[14]*b.e[ 8] + a.e[15]*b.e[12];
    matrix.e[13] = a.e[12]*b.e[1] + a.e[13]*b.e[5] + a.e[14]*b.e[ 9] + a.e[15]*b.e[13];
    matrix.e[14] = a.e[12]*b.e[2] + a.e[13]*b.e[6] + a.e[14]*b.e[10] + a.e[15]*b.e[14];
    matrix.e[15] = a.e[12]*b.e[3] + a.e[13]*b.e[7] + a.e[14]*b.e[11] + a.e[15]*b.e[15];
    return matrix;
  }

【サンプルコードの解説】
「multiply」というメソッド名は「乗算する」という意味です。
「a」引数と「b」引数は「Matrix3D」クラスのインスタンスで、行列同士を乗算したMatrix3Dクラスのインスタンスを戻り値で返します。