オブジェクトの頂点変換やピクセルを色付けするシェーダー言語「WGSL」の文法を学ぼう

はじめに

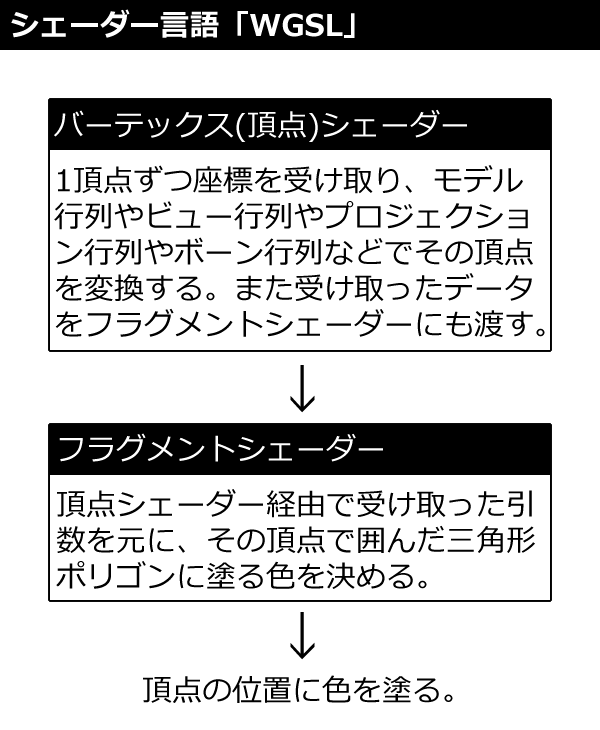
「シェーダー」とは、どの座標にどの色を塗るかを決めるためのプログラミング言語です。図1のようにまず「バーテックス(頂点)シェーダー」(以下、頂点シェーダー)が呼ばれ、そこから「フラグメントシェーダー」に値を渡してピクセルに塗る色を決めます。シェーダー自体は頂点座標を計算し、どこにどの色を塗るかを決めるだけです。

WebGPUの前身である「WebGL」ではシェーダー言語にC言語風の「GLSL(OpenGL ES Shading Language)」が使われていましたが、WebGPUではRust言語風の「WGSL(WebGPU Shading Language)」を使います。Rustの文法そのままではありませんが、Rustの文法については連載「TAURI＋Rustではじめるデスクトップアプリ開発」の第3回を参考にしてください。

WGSLでも「ベクトル」や「行列」が出てきましたが、注意して欲しいのは前々回で実装したベクトルと、前回で実装した行列をそのまま使う訳ではありません。WGSLに最初から内蔵されたベクトルや行列の関数を使います。本当は両方一緒にできたら便利なのに。

図1：WGSLの概要

頂点シェーダー

頂点シェーダーは頂点のデータだけでなく色などのデータも受け取り、頂点シェーダーを経由してフラグメントシェーダーにデータを渡します。

頂点シェーダーの文法

頂点シェーダーは次の書式のように記述します。引数は大抵複数あります。戻り値は大抵「構造体(struct)」になり、頂点シェーダー内で計算した結果が構造体に入れられて、そのままフラグメントシェーダーに送られます。

@vertex fn main(引数:型) -> 戻り値の型 {
  頂点の変形などを計算
  return 戻り値;
}

次のサンプルコードはベクトルの計算方法と行列の計算方法です。ベクトル計算の中身については第6回を、行列計算の中身については第7回を参照してください。この計算方法は頂点シェーダーだけでなくフラグメントシェーダーでも共通です。

ベクトルには三次元のvec3fだけでなくf32やvec2f、vec4fもあります。また行列には4×4のmat4x4fだけでなくmat3x3fもあります。単位行列・平行移動・回転・スケーリング・パースペクティブ・カメラ・法線行列などはシェーダーの外で作ってユニフォーム定数で持ってきます。

var v1: vec3f = vec3f(1.0, 2.0, 3.0); //三次元ベクトル
var v2: vec3f = vec3f(3.0, 2.0, 1.0); //三次元ベクトル
var v3: vec3f; //三次元ベクトル
v3 = v1 + v2; // 加算
v3 = v1 - v2; // 減算
v3 = v1 * 2.0; // 乗算
v3 = v1 / 2.0; // 除算
let f = sqrt(25.0); // 平方根
v3 = sqrt(v1); // 平方根
f = length(v1); // 長さ(大きさ)
v3 = normalize(v1); // 正規化
let d = dot(v1,v2); // 内積
v3 = cross(v1,v2); // 外積
f = v1.x; // アクセサでv1変数の0インデックスにアクセス、他にy、z(、w)
f = v1.r; // アクセサでv1変数の0インデックスにアクセス、他にg、b(、a)
f = v1[0]; // 配列でv1変数の0インデックスにアクセス、他に[1]、[2](、[3])

var m1: mat4x4f = mat4x4f(
  vec4f(1.0, 0.0, 0.0, 0.0),
  vec4f(0.0, 1.0, 0.0, 0.0),
  vec4f(0.0, 0.0, 1.0, 0.0),
  vec4f(0.0, 0.0, 0.0, 1.0)
); // 4×4行列
var m2: mat4x4f = mat4x4f(
  vec4f(1.0, 0.0, 0.0, 0.0),
  vec4f(0.0, 1.0, 0.0, 0.0),
  vec4f(0.0, 0.0, 1.0, 0.0),
  vec4f(1.0, 2.0, 3.0, 1.0)
); // 4×4行列
let v4 = m1 * vec4f(v1,1.0); // つまりvec4f(1.0, 2.0, 3.0, 1.0)、ベクトルのトランスフォーム
v3 = v4.xyz;
let m3 = m1 * m2; 行列同士の乗算
let inv = inverse(m3); // 逆行列
let t = transpose(m3); // 転置行列

頂点シェーダーのサンプル

次のサンプルコード「lib」→「WGSL.js」では、頂点をプロジェクション行列(パースペクティブ行列)、ビュー行列(カメラ行列)、ワールド行列(モデルを平行移動・回転・スケーリングした行列)で変形し、法線行列(ワールドやカメラの向きに合わせて法線の向きを決めるための行列)と計算した法線ベクトル、色ベクトル、反射強度、「VertexOutput」構造体で得たUV座標の戻り値をフラグメントシェーダーに渡します。

struct Uniforms {
  projectionMatrix : mat4x4f,
  viewMatrix : mat4x4f,
  worldMatrix : mat4x4f,
  normalMatrix : mat4x4f,
}
@group(0) @binding(0) var uniforms : Uniforms;

struct VertexOutput {
  @builtin(position) position : vec4f,
  @location(0) normal : vec3f,
  @location(1) color : vec4f,
  @location(2) specular : f32,
  @location(3) uv : vec2f
}

@vertex
fn main(
  @location(0) position: vec4f,
  @location(1) normal: vec3f,
  @location(2) color: vec4f,
  @location(3) specular: f32,
  @location(4) uv : vec2f,
  @location(5) bone : f32
) -> VertexOutput {
  var output : VertexOutput;
  output.position = uniforms.projectionMatrix *
    uniforms.viewMatrix * uniforms.worldMatrix * position;
  output.normal = (uniforms.normalMatrix * vec4f(normal,1)).xyz;
  output.color = color;
  output.specular = specular;
  output.uv = uv;
  return output;
}

【サンプルコードの解説】
「Uniforms」構造体でユニフォーム定数をシェーダー内で定数データを表現するために使います。ユニフォーム定数は描画コールの間で変わらないデータで、CPUからGPUへ送られシェーダー(頂点シェーダーとフラグメントシェーダーの両方)内で利用されます。「@group」でバインディング(接続、束縛)して「uniforms」変数として扱います。ここではプロジェクション行列、ビュー行列、ワールド行列、法線行列を持ちます。
VertexOutput構造体は戻り値の型に使います。「@builtin」はアトリビュート(属性、特性)で特定の組み込み値をシェーダーに渡すために使います。「@location」もアトリビュートで、シェーダーの入力または出力がどのパイプライン(流水管、配管)のバインディングに対応するかを示します。主にフラグメントシェーダーのカラー出力や頂点シェーダーの入力に使用されます。ここでは座標ベクトル、法線ベクトル、色ベクトル、反射強度、UV座標を持ちます。
VertexOutput構造体のoutput変数を宣言します。座標ベクトルを引数で渡された座標にユニフォーム定数の行列をかけて取得します。法線ベクトルをユニフォーム定数の法線ベクトルに引数の法線をかけて取得します。色ベクトルと反射強度とUV座標を引数から取得します。output変数を戻り値で返します。